Posted
on January 6, 2015
Jacob
was one of eight gifted mathematicians in his family (and the first)!
Born in Switzerland on this date in 1655, he so loved the logarithmic
spiral, he asked that it be carved on his gravestone, which was
erected after his 1705 death.
In
between his birth and death, Jacob Bernoulli made many contributions
to calculus, but he is most famous for his work on probability.
Here
are some of the things that Bernoulli explored, discovered, and made
contributions to:
You probably know that
infinity is endless. Well, an infinite series is the sum of
infinitely many numbers related to each other in a particular,
defined way. Here is an example:1/2 + 1/4 + 1/8 + 1/2^n
As n gets larger and
larger, the fraction ½ to the nth power gets smaller and smaller, and although it
seems that you can never QUITE get to the number 1, since there are
an infinite number of fractions added to the series, we say that the
answer converges on 1.
By the way, infinite
series are important in practical fields such as engineering and
biology!
This important number is
approximately 2.71828 but it is irrational, so the digits after the
decimal place go on and on and on and on...forever! Although it seems
impossible that this number would be important in any way, Bernoulli
discovered it when studying compounding interest (something that
banks do so that you can grow your money!).
A differential equation
states how a rate of change in one variable is related to other
variables.
Probability is simply the
likelihood of something happening. You can explore probability using
dice, cards, spinners, or colored M&Ms.
Here are some simple
questions you can ask (there are way more complicated questions!):
- If you throw one die ten times, what percent of the time will you roll a 6? How about if you throw the die ten thousand times?
- In the game 21, if you have 11 points and want to get to 21, how likely are you to get 10 points in your next card? (Face cards AND the ten-spot cards are all worth 10 points.) Obviously, it depends on how many 10's have already been played!
- If there are 30 spots on the spinner, alternating black and red, what is the likelihood of spinning a red?
- What is the likelihood of pulling out a brown M&M from a full bag of M&Ms?
Here is a really
interesting probability problem called the Monty Hall Problem.
Also
on this date:
Plan
ahead:
Check
out my Pinterest pages on:
And
here are my Pinterest boards for:
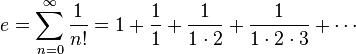
No comments:
Post a Comment