Posted
on August 26, 2014
You
know how we love celebrating Pi Day every March 14? Well, today we
can eat pie again—this time, birthday pie in honor of the fellow
who proved that pi is an irrational number!
Johann
Heinrich Lambert, born on this date in 1728, was a Swiss
mathematician, physicist, philosopher, and astronomer.
Lambert
did a lot of cool stuff in math, including working with non-Euclidean
geometry...that is, the kind of geometry that deals with curved space. He also studied conic sections and helped make the
calculation of the orbits of comets simpler.
Lambert
also studied map projections and showed that map makers could not get
BOTH the outlines of landforms AND the size (or area) of those
landforms right, because the Earth is round (almost spherical) and
maps are flat (pretty much two-dimensional).
In
physics, Lambert studied light and perspective and optics and color.
In astronomy, Lambert developed theories about the generation of the
universe and about star systems. He wrote about logic and philosophy,
and he worked with famous philosopher Immanuel Kant.
But
pi...ah, pi!
Let's
talk about pi!
What
does it mean to say that pi is an irrational number?
Rational
numbers are those that can be expressed as a fraction. The number
124 is rational because it can be expressed as a fraction:
124
1
One-half is rational because it can be expressed as a fraction:
1
2
But
pi cannot be expressed as a fraction. You may remember that pi is the
answer to the problem of dividing a circle's circumference by its
diameter. EVERY SINGLE CIRCLE – no matter what it's circumference
and diameter – when you divide the former by the latter, you come
up with the same exact number....a number that cannot be expressed as
a fraction.
(Pi
is close to 22/7 – but close is not the same as equal, in math.)
Another
way of talking about rational and irrational numbers is to explain that a rational number can
be expressed as a decimal, such as these decimal numbers:
6.78
0.34
8
(which is the same as 8.0)
0.125635895322
Some
rational numbers are not as simple as these, and they can be
represented by decimal numbers that NEVER END but instead go on and
on and on and on forever.
Here
is one:
1
3
This
rational number, one-third, can be represented by this decimal
number:
0.33333333333333333...
EXCEPT
to make it accurate, I would have to keep typing 3s forever, and you
would have to keep reading 3s forever, and neither of us would get
anything else done. Since that would be boring, we call these
decimals that go on forever “repeating decimals.” And we write
repeating decimals by either:
putting
three dots after the part that repeats,- or putting a little line over the top of the part of the decimal that repeats forever.
Here
are some more repeating decimals:
Now...that's
all rational numbers.
What
about irrational numbers?
When
you try to show an irrational number as a decimal number, the numbers
go on and on forever BUT DON'T REPEAT!
Here
is a little bit of pi:
Mathematicians
have used computers to figure out the digits of pie out to more than
10 trillion digits! And there is no repeating pattern. We can say that pi is
sorta kinda close to 3.14 – but remember, in math “close” is
not the same as “equal.”
Today's
birthday boy, Lambert, is the first mathematician to offer a
mathematical proof that, no matter how far into pi you go, there will
never be repeating decimals. In other words, he proved that the
number is irrational.
Also
on this date:
...and here
Plan ahead:
Check
out my Pinterest boards for:
And
here are my Pinterest boards for:
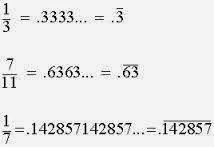
No comments:
Post a Comment